[Data] 회귀진단이란 무엇일까?

회귀진단이란 무엇일까?

들어가기

회귀 분석을 실시하기 위해서는, 기본적으로 회귀분석의 가정에 대해 고려해야 한다.

회귀 분석의 4가지 가정
I. X와 Y의 관계는 선형적인 관계이다. (선형성)
II. 잔차의 분포는 정규분포를 띄고 있다. (정규성)
III. 잔차의 분산은 동일하다. (등분산성)
IV. 잔차는 상호 독립이다. (독립성)

그러나, 이것들이 깨진다면, 어떻게 될까? 그리고 가정이 잘 성립하는지 어떻게 검토할 수 있을까?

또한, 데이터의 분포에 따라 이상치의 처리 등에 대해서도 고민해야 한다.

예를 들어, 

https://towardsdatascience.com/linear-regression-models-and-influential-points-4ee844adac6d

위와 같은 상황에서는 outlier 때문에, 예측된 직선이 위로 치우치게 될 가능성이 높다. 즉, 점 하나 때문에 예측의 정확도가 떨어질 수 있다. 

이러한 케이스를 잘 골라내어, 전체적인 경향을 잘 나타내는 설명 모델을 만드는 것이 중요할 것이기에 회귀 진단 과정이 매우 중요하다.

특이값과 이상치에 대해 확인하기

이상치가 발생하는 상황은, 축이 두 가지 이므로 두 가지 상황에 대해 고려할 수 있다.

상황 1.  x값이 전체적인 데이터 분포에 비해 지나치게 떨어져 있는 이상치
상황 2.  y값이 전체적인 데이터 분포에 비해 지나치게 떨어져 있는 이상치

그런데, 정말 두 가지만으로 이 상황을 분류해야 하는 것이 맞을까?

상황 1 : 빨간 점은, y에 대해서만 이상치이다. 이 경우, 직선을 위로 치솟게 할 수 있으므로 제거가 맞다.
상황 2 : 빨간 점은, x에 대해서만 이상치이다. 이 경우, 직선을 내리꽂게 할 수 있으므로 제거가 맞다.
상황 3 : 빨간 점은, x와 y 모두에 대해 이상치이다. 그러나, 직선의 경향성을 잘 설명해주고 있다.

이 세 가지 상황에 따라, 우리는 빨간 점을 다르게 해석해야 할 것이다. 이와 관련된 지표를 살펴보자.

레버리지

레버리지란, 회귀 직선에 얼마나 영향을 주는 점인지를 측정해주는 지표로 쓰이게 된다.

레버리지는 Hat-value에 의해서 유도가 되는데, 기본적으로 다중 선형회귀에서 얻게되는 행렬에서 시작된다.

여기서 H를 Hat Matrix라고 하는데, 레버리지는 이 행렬의 '대각 성분'으로 정의하게 된다.

레버리지가 큰 데이터는 제거하거나 포함함에 따라, 회귀분석의 결과에 큰 영향을 주게 된다.

Remark > Cook's distance

레버리지도 크고, 잔차도 큰 경우를 제외하는 것이 중요할 것이다. 이럴 때 고려할 수 있는 것이 Cook's distance이다.

잔차에 대해 확인하기 - 오차의 분산과 정규성 확인하기

오차의 분산이 동일하지 않는다면?

오차의 분산이 동일하지 않다는 것의 의미는, 한 부분에서의 오차가 다른 부분에 비해 매우 크거나 작다는 것을 의미한다.

https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=yonxman&logNo=220950614789

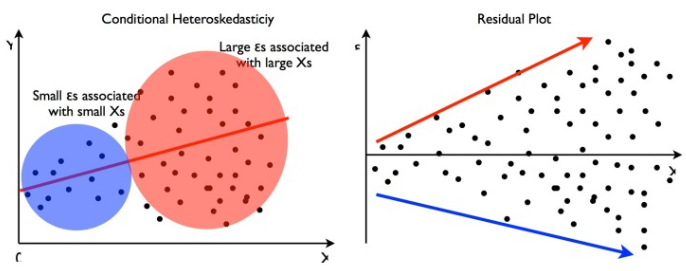
특히 이렇게 될 경우 x값이랑, 잔차와의 상관관계 또한 발생하게 되어, 해석에 문제가 발생하게 된다.

잔차의 정규성이 성립하지 않는다면?

이러한 상황을 예시로 들 수 있다. 즉, 잔차가 굉장히 균등하게 특정 부분에 몰려 있는 상황이다. 데이터의 분포를 보면 회귀분석을 사용하기에 알맞지는 않은 상황임을 알 수 있다. 이러한 경우에도 회귀분석을 하기에는 좋지 않다.

Remark> 잔차의 정규성 확인은 정규분포 확인 검증이나 Q-Q Plot을 통해 진행 가능.