들어가기
분류 문제에서, 선형 분류로 풀 수 없는 상황이 여럿 존재할 것이다.
이를 해결 할 수 있는 방법 중 하나가 Kernel Trick이다.

다음과 같이, 일차원 상에, 데이터가 놓여있다고 하자, 초록색 데이터와 파란색 데이터는 선분 하나만으로는 구분할 수 없다. 하지만, 여기에 차원을 추가하면 어떻게 될까? 즉
x -> {x, x^2}
으로 보내는 mapping을 고려하자.

2차원으로 보낸 순간, 빨간 구분선을 기준으로, 초록색 데이터와 파란색 데이터의 구분이 가능해졌다.
이렇게 쉬운 상황만 고려하면, 좋을텐데, 문제는 일반적으로는 mapping 이 되는 함수를 찾기가 매우 어렵다는 것이다.
Kernel이란?
Kernel 이란, mapping 이후에도 "내적"의 값을 유지시켜주는 함수를 의미힌다.

자주 쓰이는 Kernel 함수의 예시는 다음과 같다.
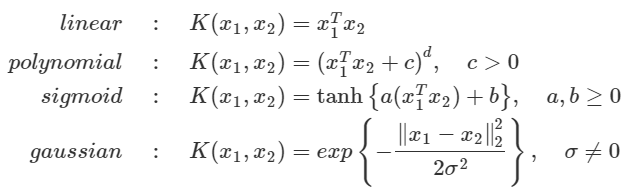
Kernel Trick, 그리고 왜 갑자기 내적 이야기가 나오는가?
갑자기 왜 내적이 튀어나왔는가, 그리고 Kernel Trick이 뭔지를 한번 생각해보자.
우선, Kernel은 위의 내용과 정의만 보면, 고차원으로 매핑시키며, 내적도 한번에 실시해주고 있다.
즉, 다시 말해 Kernel은 데이터를 어디에 매핑했는지, 그 구성은 어떤지, 내적은 어떤지는 아무튼 관심 없고, 최종 결과값을 같게 해주는데에 집중하고 있다. 이렇게 할 경우, 매핑 함수를 구하는 과정도, 내적의 복잡한 계산량도 줄어든다는 장점이 존재한다.
하지만, 그래도 문제가 하나 있는데, "내적"이 왜 튀어 나왔는지에 대해서는 아직도 답하진 않았다.
이는, SVM을 생각해보면, 답을 얻을 수 있다.

결정 경계를 구하는 문제로, 다시 돌아오면 SVM의 궁극적인 목적은, 최적의 결정경계를 찾는 문제인데, 최적의 결정경계는 Margin, 즉 각 class의 원소 중 결정경계와 가장 가까운 원소와의 거리를 최대화 하는 것이다.
그리고 이 거리는 내적을 통하여 구할 수 있기 때문에, 내적 값을 구해두는 과정이 반드시 필요하다!
'Archive > TIL' 카테고리의 다른 글
| [TIL] 0808 아침스터디 - 다차원척도법 (MDS) (0) | 2022.08.08 |
|---|---|
| [TIL] 0805 아침스터디 - 나이브 베이즈 복습 (0) | 2022.08.05 |
| [TIL] 0725 아침스터디 - ROC curve, 비용민감 곡선 (0) | 2022.07.25 |
| [TIL] 0713 아침스터디 - hyperparameter tuning(2) (0) | 2022.07.13 |
| [TIL] 0711 아침스터디 - Hyper Parameter tuning(1) (0) | 2022.07.11 |



