
문제 설명
주어진 조건에 맞는 814개의 점을 찾아야 합니다. 주의사항은, 가장 가까운 두 점의 쌍이 여러개여서는 안 된다. 입니다..
즉, 단순히 직사각형으로 점들을 배치했다가는 가장 가까운 두 점의 쌍이 여러개이므로 오답! 입니다.
생각의 단계
1단계. 일단 풀기
먼저 가장 쉽게 생각할 것은, 임의로 점을 뿌리면 두 점의 거리가 같은 쌍이 두 개 이상 나올 가능성이 매우 적습니다. 이렇게 하면 일단 정답은 맞힐 수 있습니다.
import random
for i in range(814):
a=random.randint(-8140,8140)
b=random.randint(-8140,8140)
print("%d %d"%(a, b))
하지만 이대로는 고득점을 맞기는 어렵겠죠? 점수를 더 높혀봅시다. 어떻게 해야 가장 멀어질까요?
2단계. 문제 조건에서 역발상하기.
역발상으로 2개의 점만 가까워 지게 만들면 되므로 나머지 812개의 배치를 생각해 봅시다.
812는 28*29 입니다. 28*29가 가장 잘 되게 직사각형으로 최대한 넓게 퍼트리고, 그 변의 길이보다 짧게 만들면 되네요.
실제로 이 간격을 계산해보면 한 변의 길이가 542인 정사각형으로 배치해야만 28 * 29 형태로 812개를 배치할 수 있습니다.
그러면, 마지막 두 선의 길이가 541이면 되겠네요. 541점입니다. 축하합니다.!
# 가장 가까운 애만 한 쌍 나오면 된다.
# 나머지 812개는 최대한 멀리 배치한다.
# 남는 공간을 붙이고, 가능한 만큼 효율을 뽑으면 541점
for i in range(-8140, 7036, 542):
for j in range(-8140, 7578, 542):
print("%d %d"%(i, j))
print("%d %d"%(8140, 8139))
print("%d %d"%(7599, 8139))

조금 더 점을 밀집해서 보관해주면, 굳이 두 개의 점이 아니어도 좋지 않을까요? 사실 1개의 점만 틀어주면 최단거리의 유일성은 보존할 수 있습니다. 즉 813개의 점을 최대한 효율적으로 균일하게 배치하는 방법을 생각해봅시다. 직사각형을 좀 더 응용해볼까요?
3단계. 격자 형태로 배치하기.
격자 형태로 배치하면 조금 더 넓게 점들을 배치할 수 있습니다. 이런식이죠.
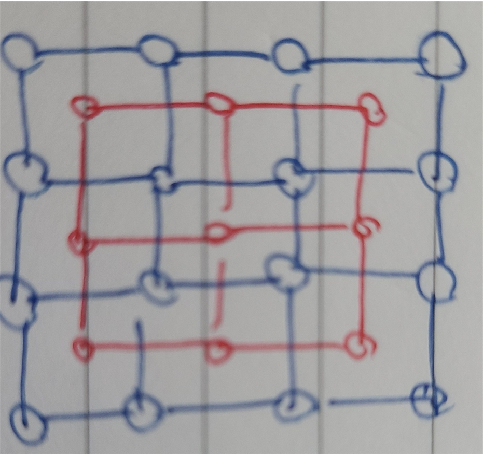
이러면 제한된 공간 내에 더 많은 점들을 균일하게 배치할 수 있겠네요. 마지막으로 들어가는 점만 살짝 틀어줍시다.
근데, 몇 개의 점을 외부에 배치해야 내부가 가장 적합할까요?
정사각형 배치를 위해 제곱수를 계산해보면
19 * 19 = 361, 20 * 20 = 400, 21 * 21 = 441....
361+400은 부족합니다. 400+441은 조금 점이 많네요.
다음 직사각형 배치도 고민해봅시다. 가로, 세로에 들어가는 개수 차이가 적을수록 좋으니 차이가 1일때만 고민합시다.
19*20 = 380 20*21 = 420, 21*22 = 462.....
380+420은 부족합니다. 420+462는 점이 너무 많이 남네요.
이 과정에 따라, 정사각형으로 배치하기로 결정합시다. 물론 더 엄밀하게 최대치를 찾을 수 있겟지만 우선 여기서 이대로 합시다.
우선 테두리를 따라 최대한 넓게 21 * 21 형태로 배치합니다. 21 * 21 각 칸의 중앙점에 20 * 20으로 최대한 배치하되 마지막 814번째 점의 x좌표, y좌표를 1정도씩 차이나게 해줘, 가장 가까운 점이 유일하게 만들어 줍시다.
그럼 길이가 대충 어느정도 나오냐고요? 피타고라스의 정리에의해 (16280/20)/루트2 보다 살짝 적게 나오겠네요!
# 랜덤을 고려하지 않는 풀이 2
# 더욱 효율로 간다.
# 아예, 변에 붙여서 441개 / 나머지를 최대한 채운다.
count = 0
for i in range(-8140, 8141, 814):
for j in range(-8140, 8141, 814):
print("%d %d" %(i, j))
count += 1
for i in range(-7733, 7734, 814):
for j in range(-7733, 7734, 814):
if count <= 812:
print("%d %d" %(i, j))
count += 1
print("%d %d" %(7732, 7734))정사각형 배치를 한 결과의 점수는 574.17점으로 30점이나 더 올릴 수 있었습니다. 와!!! 이젠 정말 만족!

4단계. 모양의 효율화
굳이 왜 정사각형이어야 할까요? 다음과 같은 배치가 좀 더 효율적이지 않을까요?

정삼각형 배치를 생각해 볼 수 있습니다.....?
문제가 있네요. 한 변의 길이가 언제 최적일지 알 수 있을까요? 변이 너무 길면 814개보다 부족할 것이고, 변이 너무 짧으면 814개보다 너무 많이 점이 담길 것입니다. 딱 814개가 최적인 변의 길이를 찾아봅시다.
정삼각형의 높이를 구해봅시다. 정삼각형의 높이는 중학교 때 피타고라스 정리의 응용 때 배웠습니다. (루트3 / 2) * a 입니다.
전체 판의 길이는 16280이므로, 높이와 너비가 몇 개씩 들어가는지를 기준으로 하여 계산하면 되겠습니다.
여기서 문제가 되는 부분은 현재 가로줄은 두 종류가 있습니다.

빨간색 부분과 파란색 부분이 반복되고 있습니다. 파란색 부분이 1개의 점을 더 많이 차지합니다.
우선 빨간색 부분으로 시작하여 빨간색 부분으로 끝나게 배치를 해본다고 가정을 해 보고, 들어가는 점의 개수를 계산해 봅시다.
a = 1
while True:
red = (16280//a) * ((16280 // ((3 ** 0.5) * a)) + 1)
bule = (16280//a + 1) * (((16280-(a * (3 ** 0.5))) // ((3 ** 0.5) * a)) + 1)
if red + blue < 814:
break
a += 1
print(a)빨간색 부분이 세로로 몇번 들어가는지, 가로로 몇 번 들어가는지를 정삼각형을 기준으로 계산했습니다. 이 때 처음으로 814개가 부족해지는 현상이 언제 일어나는지를 확인했습니다. 이 때의 값은 a=627입니다. 즉 한 변의 길이는 626인게 가장 효율적이군요.
그럼 이제 역산이 필요합니다. 모두 정수점이므로, 실제로는 정삼각형일 수는 없고 이등변삼각형 형태이여야 할 겁니다. 즉 높이가 몇개인지, 가로가 몇개인지를 세야 합니다.
가로의 간격은 총 26개로, 파란색 부분의 점의 개수는 총 27개입니다. 빨간색 부분의 점의 개수는 26개 입니다.
한 변의 길이가 626인 정삼각형의 높이는 약 542.1xxx 가 나옵니다. 위의 그림에서 빨강 ~ 빨강의 세로 길이는 1084가 되겠네요.
삼각형의 높이를 541로 두고 배치를 해 봅시다. (개수는 직접 세 봅시다. 딱 점이 알맞게 조금 넘치는 정도입니다.)
count = 0
# 윗꼭지점부터 배치
for i in range(-8140+313, 8140-312, 626):
for j in range(-8140, 8141, 1084):
count += 1
print("%d %d" %(i, j))
# 나머지 꼭지점 배치
for i in range(-8140, 8141, 626):
for j in range(-8140+542, 8141, 1084):
count += 1
if count < 814:
print("%d %d" %(i, j))
elif count == 814:
print("%d %d" %(i, j-1))
break이렇게 배치를 하여 돌려보면 625.02점이라는 매우 높은 점수를 얻을 수 있습니다!
이 문제의 현재 최고기록은 약 625.88점입니다. 이 값이 이론치인 것으로 보입니다. 아마 이 값을 맞기 위해선 위의 풀이에서 공간이 낭비되는 부분을 줄이거나 어떤 배치를 할지 등의 조정이 더 들어가야 할 것으로 보입니다. 실제로 삼각형의 높이 부분이 낭비되고 있으니까요. 이를 줄이면 어느정도 더 높은 점수가 나올 것으로 보입니다. 실제로 몇 번째 높이냐에 따라서 일차부등식을 세워서 높이를 1~2 높여도 되는 부분은 어디인지, 찾을 수 있을 것입니다만... 굳이 거기까지 더 갈 이유는 없을 것 같습니다.
시작은 브론즈1의 간단한 문제지만, 최적화를 하면서 다양한 풀이법을 생각해 볼 수 있던 좋은 문제였습니다!
'알고리즘 & PS' 카테고리의 다른 글
| [BOJ] 퍼즐 (1525, G2) (4) | 2024.12.15 |
|---|---|
| [BOJ] 성냥개비 (3687, G2) (1) | 2024.12.02 |
| [BOJ] 욕심쟁이 판다 (1937, G3) (1) | 2024.11.28 |
| [BOJ] 가장 큰 정사각형 (1915, G4) (0) | 2024.11.25 |
| [BOJ] n제곱 계산 (12728, P1) (0) | 2024.11.25 |



