빈도주의와 베이지안
확률에 대한 의미를 해석하는 관점은 크게 두 가지가 있다.
빈도주의
빈도주의는 반복적으로 선택된 표본이 사건의 원소가 될 경향을 나타내다.
예를 들어, 주사위를 던져서 1이 나올 확률이 1/6이라는 것은, 빈도주의의 관점에서는 실제로 주사위를 던져 나온 횟수 에 확률을 곱한 값 만큼 해당 사건이 발생한다고 본다. 더 나아가서, 빈도주의 관점에서 확률은 시행을 무한히 반복한다고 가정하여, 특정 사건이 일어난 비율의 수렴값을 뜻한다.
베이지안
반면 베이지안의 경우는 특정 사건이 일어날 확신이 어느정도 있는가를 수치적으로 표현한 것이다. 다시 말해, 선택한 표본이 특정 사건에 속할 신뢰도를 의미한다.
예시) 동전을 하나 던져 앞면이 나올 것이라는 확신은 50%다.
이러한 베이지안의 관점은 베이즈 정리로부터 나온다.
베이즈정리
베이즈 정리는 다음과 같다.

- 사전확률 : P(A)에 해당한다. 사건 B에 대한 정보가 주어져 있지 않다.
- 사후확률 : B라는 사건의 정보가 업데이트 되며, P(A|B)를 얻게 된다.
- 가능도 : P(B|A)에 해당하는 부분으로, 사건 A가 B를 지지할 가능성을 의미한다.
- Pr(B)는 상수 역할을 하게 된다.
베이즈 정리에 기반하여 확률 분포를 해석해보는 것이 베이즈 추정법이다.
베이즈 추정법 및 기본원리
베이즈 추정법
확률분포함수 모수를 μ라 하고 모수를 추정하는 상황을 고려하자.
- 최대가능도 추정법 : 모수를 상수로 본다.
- 베이즈 추정법 : 모수를 확률변수로 본다. (어떤 값이 가능성이 높고, 어떤 값이 가능성이 낮은가?)
즉, 베이즈 추정법에서는 어떤 값 하나로 단정짓지 않는다는 의미이다.
베이즈 추정법의 기본 원리
베이즈 추정법은 다음과 같이 계산한다.
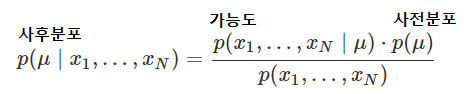
- 사전분포 : 모수의 사전 분포, 베이지안 추정 작업을 하기전에 이미 알고 있던 μ에 대한 분포이다.
- 사후분포 : 모수의 사후 분포, xi 라는 데이터가 주어질 때의, μ에 대한 분포로 이를 구하고자 한다.
- 가능도 : 모수가 주어질때, xi가 나올 수 있는 확률값을 의미한다.
베이즈 추정의 예시
베이즈 정리의 예시를 확인해보자.
베르누이 분포의 모수 추정
이산확률변수인, 베르누이 분포의 모수를 베이즈 추정법으로 추정해본다.
베르누이 분포의 사전분포는 베타분포라고 가정하자. 이때 a = b = 1 이라고 가정하자.


베이즈 정리를 사용하여 x1~xn 정보가 주어질때의 μ를 추정하자.

여기서 사전 분포와 사후 분포는 모수a, b의 값만 다르고 형태는 동일한 확률밀도 함수로 표현이 된다. 이러한 분포를 켤레 사전확률분포라고 한다. 여기서는 다음과 같이 갱신된다.

이 과정을 바탕으로 사전 분포에서 모수 값을 갱신하여 사후 분포를 얻게 된다.
정규분포의 모수 추정
정규분포의 기댓값 모수를 베이지안 방법으로 추정할 수 있다. 분산은 이미 안다는 가정이다.
모수의 사전 분포는 정규분포를 사용한다.
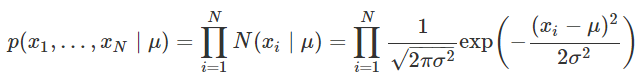

'Archive > 수학 & 통계학 관련' 카테고리의 다른 글
| [Stat] 집단간 평균 비교 (0) | 2021.09.03 |
|---|---|
| [Data] 선형회귀에서의 변수 선택(AIC, VIF) (0) | 2021.08.07 |
| [Prob] 베타분포와 디리클레분포 (0) | 2021.06.07 |
| [Cal] Matrix Calculus Review (0) | 2021.06.03 |
| [Prob] 우도(가능도) 최대우도 추정법 (0) | 2021.05.27 |


