들어가기
서비스 분석에서 유저의 이탈을 예측하는 것은 중요합니다.
- 특정 이벤트에 의해 유저의 이탈/비이탈이 나눌 경우, 해당 이벤트의 경험 여부를 결정할 수 있다.
- LTV의 예측에서는 유저의 수명과 가치의 곱으로 계산되기에 유저의 수명 또한 고려해야 한다.
즉 이탈을 탐지하고 고려하는 것은 중요한데, 여기서 이탈에 대해 고려할 것은 두 가지입니다.
- 이탈을 할 유저인가?
- 이탈을 한다면 언제 할 것인가?
물론, 장기적 관점에서는 결국 이탈을 할 수 밖에 없겠습니다.(일단 사람의 수명이 무한대가 아닌 이상 이탈은 수학적, 생물학적으로 확정이다.)
이탈의 탐지도 중요하나, 언제 이탈을 할 것인지에 대해 예측하는 것에 한번 초점을 두겠습니다. 여기서 이제 생존분석 이라는 것을 도입해볼 수 있습니다.
기본 개념
생존분석(Survival Analysis)이란, 특정 사건의 발생 시점을 예측하는 것을 목표로 합니다.
여기서 사건이란 생존의 반대 개념을 의미합니다. (의학 - 죽음, 공정 - 사고, 서비스 - 이탈)
가장 기본적인 용어들을 살펴보면 다음과 같습니다.
- 사건 : 생존의 반대 개념
- 시간 : 대상 관찰 시점으로부터 경과 시점 (이탈 분석 - 가입 후 경과 시점)
- 생존함수 : 고객이 특정 시간보다 더 오래 잔존해 있을 확률을 계산하는 함수
- 위험함수 : 고객이 특정 시간 t에 이탈할 확률을 계산하는 함수
- 누적위험함수 : 고객이 특정시간 t까지 이탈했을 확률, 즉 위험함수를 0에서 t까지의 구간으로 적분
실습을 통한 이해
https://github.com/swtaktak/TIL_new/blob/main/data_analyst_practice/240124%20Survival_Analysis%20Basic.ipynb
전체 코드는 위 링크를 통해 확인 가능합니다.
간단한 데이터를 바탕으로 어떤 방식으로 진행하는지 알아보겠습니다.
* 지금은 수학적, 통계적 이해보다는 무엇을 했는지에만 집중하도록 하겠습니다.
주의 사항 : 유저의 생존 곡선을 그리기 위해서는 유저의 생존 시간에 대한 자료가 필요하다.
Kaggle Link : https://www.kaggle.com/datasets/blastchar/telco-customer-churn
통신사 이탈과 관련된 Kaggle의 데이터로 실습을 진행하였습니다.
Part 1. 생존함수 그리기
Q. 우리 서비스에 고객이 들어오면 얼마나 빨리 이탈할까요?
"평균적"으로 고객이 얼마나 이 서비스에 살아남을 수 있을지 전체적인 지표를 확인해 보겠습니다.
from lifelines import KaplanMeierFitter
kmf = KaplanMeierFitter()
kmf.fit(df["tenure"], df["is_churn"])
plot = kmf.plot_survival_function()
plot.set_xlabel('time (month)')
plot.set_ylabel('survival function')
plotKaplan-Meier Estimation 이라는것을 사용한다고 합니다. 이론적 배경은 추후에 살펴보고 그래프를 한번 보면 다음과 같습니다.

시간이 지날수록, 곡선이 하향하고 있습니다. 20개월 정도가 지나면 평균적으로 80%정도의 고객만이 남아있다고 해석할 수 있습니다. 연한 부분은 신뢰구간입니다. 신뢰 구간을 설정하기 나름이지만, 기본 세팅은 95%라고 합니다.
Part 2. 집단간 비교하기
Q. 평균적인건 잘 봤는데, 그게 무슨 의미가 있죠? 집단간 비교가 가능할까요?
두 그룹의 생존함수를 비교하여 유의미한 차이가 있는지 또한 볼 수 있습니다. 여기서는 logrank_test라는 것을 사용한다고 합니다. 역시 통계적인 내용은 추후에 살펴보고, 오늘은 쓰임새만 보겠습니다.
Example) 위의 데이터에서 남성과 여성의 이탈율에는 유의미한 차이가 있을까요?
kmf = KaplanMeierFitter()
kmf.fit(df_male['tenure'], df_male['is_churn'], label="male")
ax_kmf = kmf.plot()
kmf.fit(df_female['tenure'], df_female['is_churn'], label="female")
ax_kmf = kmf.plot(ax=ax_kmf)
ax_kmf.set_xlabel('time (month)')
ax_kmf.set_ylabel('survival function')
ax_kmf이런식으로, 두 개의 생존함수를 한 화면에 그릴 수 있습니다. 그래프를 살펴보면 다음과 같습니다.

시각적으로만 보면 여성의 이탈율이 조금 더 커보입니다만, 정말 이게 의미있는 차이긴 할까요? 통계적으로 유의미한지 확인해봅시다.
from lifelines.statistics import logrank_test
logrank_test(df_male["tenure"], df_female["tenure"], df_male["is_churn"], df_female["is_churn"]).p_valuep-value는 0.468 정도로 나옵니다. 유의수준 5% 하에서, 귀무가설을 기각할 수 없겠네요. 즉, 통계적으로 유의미한 차이라고 볼 수 없습니다! 따라서 이탈율 차이가 있다고 보긴 어렵겠네요. 다른 유의미한 지표를 찾아서 이탈율 차이가 발생한다면 개선 포인트로 잡아볼 수 있겠습니다.
Part 3. 이탈 예측 모델
Q. 좋아요, 근데 그러면 우리 서비스의 어떤 부분이 이탈을 가장 많이 일으키는지도 알 수 있을까요?
지금까지는 평균적인 수치로 생존함수를 계산했다면, 각 변수별로 이를 예측할 수도 있지 않을까요? 이럴 때 사용하는 것이 Cox-Proportional Hazards model 이라고 합니다. 역시 우선은 쓰임새만 살펴보겠습니다.
Remark. 이걸 쓸려면 일단 수치형변수여야 합니다. 범주형 변수들은 모두 0-1을 해줍시다.
* 예제에서는 일부 변수만 사용하여 데이터를 만들었습니다. 그 과정 또한 기술하겠습니다.
from lifelines import CoxPHFitter
df_columns = ['SeniorCitizen', 'Partner', 'Dependents',
'PhoneService', 'PaperlessBilling',
'tenure', 'is_churn']
df_new = df[df_columns]
df_modify = ['Partner', 'Dependents', 'PhoneService', 'PaperlessBilling']
for c in df_modify:
df_new[c] = df_new[c].apply(lambda x: 1 if x == 'Yes' else 0)
# 전체 분석 데이터, 기간을 나타내는 데이터, 이탈 라벨 데이터를 부여한다.
coxph = CoxPHFitter()
coxph.fit(df_new,
duration_col = 'tenure',
event_col = 'is_churn',
show_progress=True)이렇게 학습하면 예측 모델에 적용해야 겠죠. 예측은 이탈을 해본적이 없는 유저를 대상으로 하는 것이 의미있을 것입니다.
df_condi = df_new.is_churn.apply(lambda x: False if x is True else True)
df_notchurn = df_new.loc[df_condi]
df_notchurn_year = df_notchurn['tenure']
predictions = coxph.predict_survival_function(df_notchurn,
conditional_after = df_notchurn_year)예측 결과는 다음과 같은 형식으로 저장됩니다.

다음과 같이 이탈하지 않은 각 유저별의 생존확률을 구할 수 있다. 근데 이렇게 된 것은 어떤 수식을 얻어서 일텐데,
이를 정리해서 보는 방법도 존재한다.
coxph.print_summary()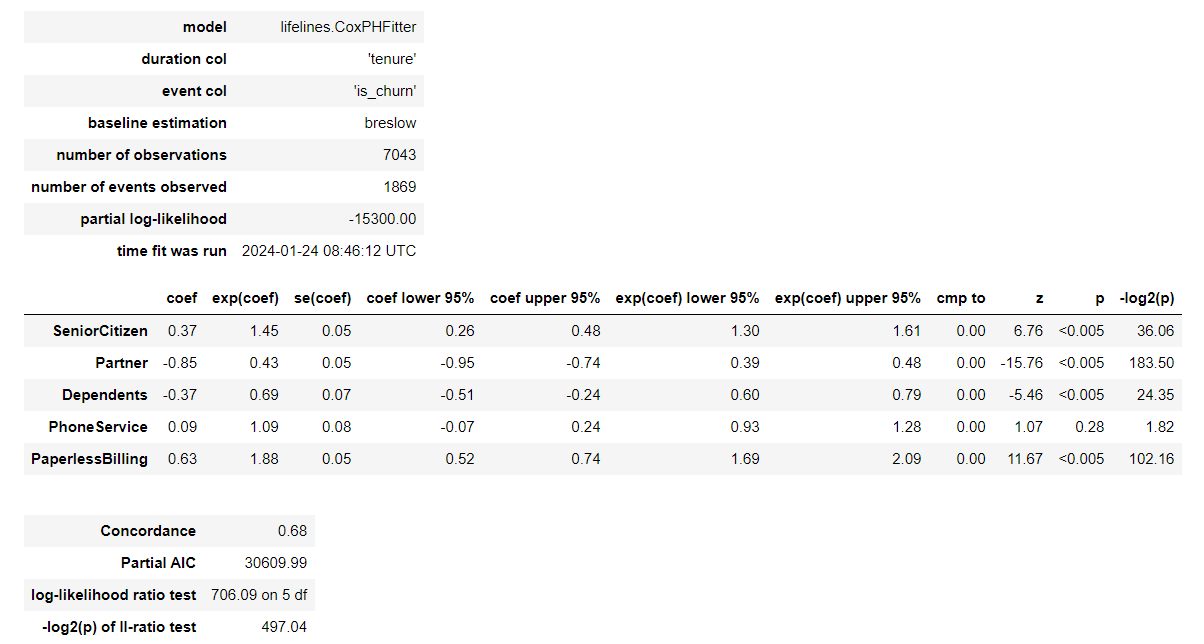
이런, 정확한 수식을 알아야 계수의 의미를 정확하게 파악할 수 있을 것으로 보입니다만, 계수가 음수면 부정적인 방향, 계수가 양수면 긍정적인 방향일 것이라는 것은 예측이 됩니다. 또한 p-value가 큰 값들은 이탈에 큰 영향이 없는 요인이라는 것도 그동안의 경험을 통해 알 수 있습니다. 하지만 이 예측 방법의 정확한 식을 알아야만 정확한 해석이 가능할 것입니다.
아무튼, 이렇게 어떤 흐름으로 데이터를 해석할 수 있을지 간단한 방법을 보았습니다. 이 이외에도 머신러닝 방법등을 활용하여 이탈 시점이나 이탈 여부 등 또한 예측할 수 있을 것입니다. 오늘 글에서는 간단한 개괄적인 내용만 파악하였습니다. 추후 글에서는 설명을 생략한 수학적/통계학적 내용을 보충하도록 하겠습니다. 수학파티
'Archive > 데이터 분석 관련' 카테고리의 다른 글
| [Data] 업리프트 모델링이란? - 예제편 (0) | 2024.01.29 |
|---|---|
| [Data] 업리프트 모델링이란? - 개념편 (0) | 2024.01.29 |
| [Data] RFM 분석이란? (실전편) (1) | 2024.01.19 |
| [Data] RFM 분석이란? (이론편) (0) | 2024.01.17 |
| [Data] A/B Test 사용해보기 : Cookie-Cats (0) | 2024.01.16 |


